Neuronen in neuronalen Netzwerken verstehen Teil 1: Künstliche Neuronen
über
Künstliche Intelligenz (KI) und maschinelles Lernen (ML) sind zwei der heißesten Themen in der Branche. Dank spektakuläre Erfolge, zum Beispiel, dass KI die weltbesten Go-Spieler besiegt hat [1], und Misserfolgen wie den Unfällen mit autonomen Fahrzeugen [2] ist der Begriff KI zu einem populären Ausdruck geworden. Während KI und ML dank Cloud-basierter Tools wie TensorFlow für die Allgemeinheit anwendbar wurden, können diese riesigen, leistungsstarken Plattformen undurchdringbar erscheinen, wenn man versucht zu verstehen, wie ML „unter der Motorhaube“ funktioniert. In dieser Reihe über neuronale Netzwerke gehen wir zurück zu den Grundlagen und erforschen den Grundbaustein der meisten dieser Systeme, das neuronale Netzwerk. Dabei helfen uns viele Beispiele zum Ausprobieren, Beispiele für coole und obskure ML-Projekte, und am Ende werden wir sogar einen Arduino mit einem „Gehirn“ ausstatten.
Computing-Herausforderungen
KI und ML sind die Computing-Herausforderungen unserer Zeit. KI, bei der es darum geht, mit Hilfe von Computern die menschliche Intelligenz nachzuahmen, und ML, das auf Mustererkennung von (halb-) strukturierten Daten abzielt, beanspruchen jährlich beträchtliche Investitionen - von Forschungsprojekten bis hin zur Entwicklung in der Halbleitertechnologie und in Computerplattformen. Und dank „der Cloud“ ist die Technologie für diejenigen, die ihre Ideen erforschen und testen wollen, leicht zugänglich.
Aber wie funktionieren all diese cleveren Algorithmen? Wie lernen sie? Was sind ihre Grenzen? Und ist es möglich, mit den Grundlagen von ML herumzuspielen, ohne sich für (noch) einen weiteren Cloud-Dienst zu registrieren? Genau diese Fragen werden in dieser kurzen vierteiligen Artikelreihe behandelt:
- Teil 1 - Künstliche Neuronen: Wir beginnen in den 1950er Jahren und sehen uns die frühen Forschungen zur Entwicklung eines künstlichen Neurons an. Wir bewegen uns schnell zu einer Software-Implementierung eines Multilayer-Perzeptrons (MLP), das Backpropagation zum „Lernen“ verwendet.
- Teil 2 - Logische Neuronen: Eine der Herausforderungen bei frühen Neuronen war ihre Unfähigkeit, die XOR-Funktion zu lösen. Wir untersuchen, ob unser MLP dieses Problem lösen kann und zeigen, wie das Neuron lernt.
- Teil 3 - Praktische Neuronen: Wir wenden unser MLP auf einen Teil des Problems des autonomen Fahrens an, der Erkennung des Zustands von Ampeln mit Hilfe eines PC-basierten Programms.
- Teil 4 - Eingebettete Neuronen: Wenn es auf einem PC funktioniert, könnte es dann auch auf einem Mikrocontroller funktionieren? Wir erkennen Ampelfarben mit einem Arduino und einem RGB-Sensor.
Lazy Learning
Lernen ist harte Arbeit für Menschen und scheinbar auch für KI. Untersuchungen der TU Berlin, des Fraunhofer HHI und der SUTD ließen die KI-Systeme ihre eigenen Entscheidungsstrategien erklären [13]. Die Ergebnisse waren verblüffend. Die KIs erfüllten nicht nur alle ihre Aufgaben bewundernswert, sondern zeigten dabei auch eine atemberaubende Cleverness in ihrer Entscheidungsfindung. Ein Algorithmus erkannte korrekt die Anwesenheit eines Schiffes in einem Bild, begründete seine Entscheidung aber mit der Tatsache, dass sich Wasser auf dem Foto befand. Ein anderer erkannte korrekt, dass Bilder Pferde enthielten, stützte seine Entscheidung aber auf eine Copyright-Markierung in einigen Bildern, anstatt die visuellen Attribute eines Pferdes zu lernen.
Kleine Geschichte der Neuronen
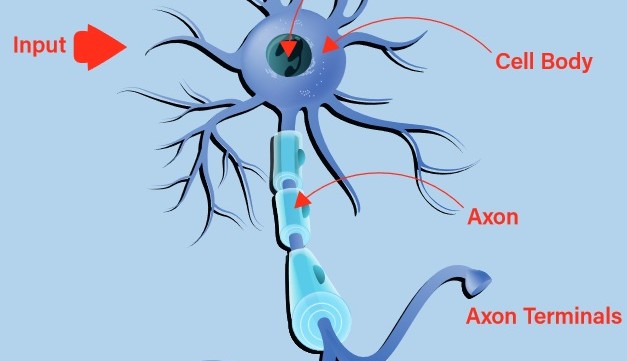
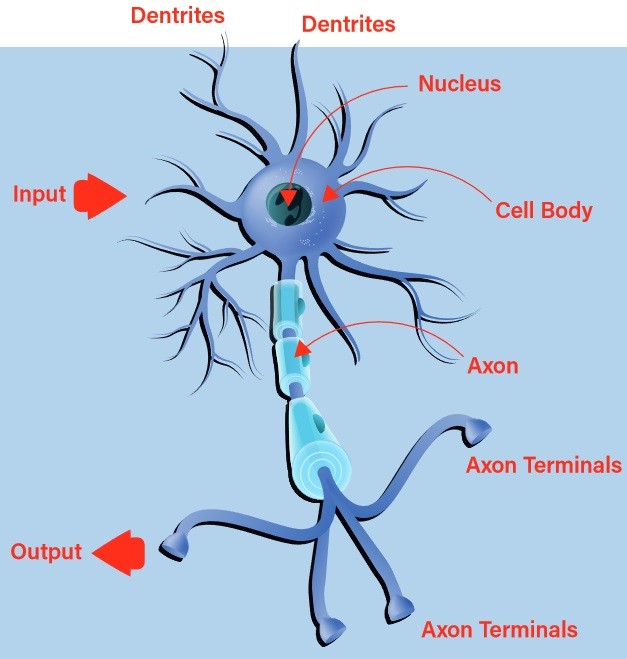
Frühe Versuche, ein digitales oder künstliches Neuron zu erstellen, orientierten sich an der Natur. Das biologische Neuron nimmt Eingaben über seine Dendriten auf und gibt die daraus resultierende Ausgabe über sein Axon an die Axon-Ausgänge weiter (Bild 1). Die Entscheidung, ob ein Reiz über den Ausgang abgegeben wird, das so genannte Feuern des Neurons, erfolgt durch einen Prozess, der als Aktivierung bezeichnet wird. Entsprechen die Eingaben einem gelernten Muster, feuert das Neuron, andernfalls nicht. Es ist schnell zu erkennen, dass Ketten miteinander verbundener biologischer Neuronen sehr komplexe Muster erkennen können.
Die ersten künstlich entwickelten Neuronen waren McCulloch-Pitts-Netzwerke, auch bekannt als Threshold Logic Units (TLU). Diese einfachen „Entscheidungsmaschinen“ konnten die Funktion von Logikgattern nachahmen, akzeptierten und gaben nur logische Werte von 0 und 1 aus. Um diese Fähigkeit zur Mustererkennung zu nutzen, mussten für jeden Eingang mathematisch oder heuristisch Gewichtungswerte bestimmt werden. Manchmal wäre auch ein zusätzlicher Eingang erforderlich (Bild 2, UND- und ODER-Verknüpfungen).
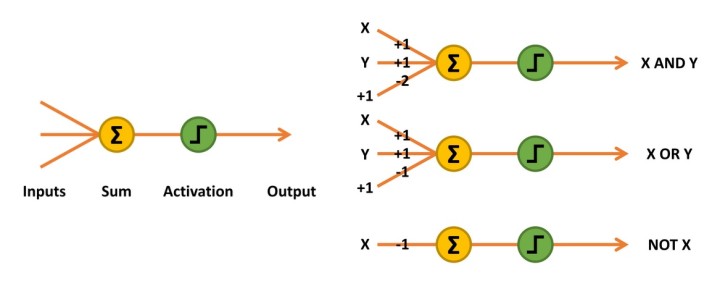
Bild 2. Das McCulloch-Pitts-Netzwerk summiert die Eingänge, multipliziert mit ihrer Gewichtung auf und aktiviert einen Ausgang, wenn das Ergebnis gleich oder größer als 0 ist.
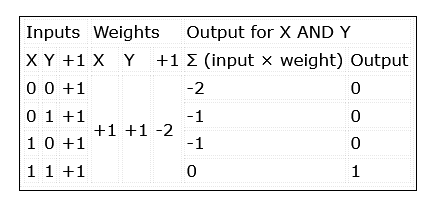
Die Eingänge des Netzes werden also einfach mit ihrer Gewichtung multipliziert und aufsummiert. Die Entscheidung, eine 1 auszugeben (den Ausgang zu aktivieren), wird über eine lineare Schwellwert-Einheit realisiert. Wenn das Ergebnis gleich oder größer als 0 ist, wird eine 1 ausgegeben, ansonsten eine 0 (Tabelle 1).
Perzeptronen
Die nächste Stufe der Entwicklung wurde in den 1950er Jahren mit der Arbeit des Psychologen Frank Rosenblatt [3] beschritten. Sein Perzeptron behielt die binären Eingänge und die lineare Schwellwert-Entscheidungseinheit der McCulloch-Pitts-TLU bei. Die Ausgabe war also ebenfalls ein binärer Wert von 0 oder 1, unterschied sich jedoch in zweierlei Hinsicht: Der Schwellwert Theta (Θ) für die Entscheidung über den Ausgabewert war einstellbar, und es wurde eine begrenzte Form des Lernens unterstützt (Bild 3).
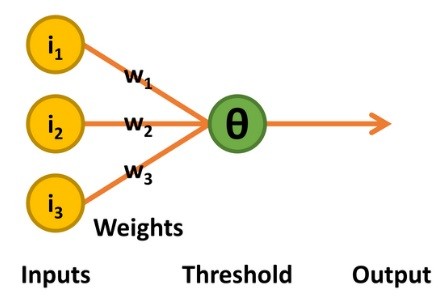
und verwendete einen iterativen Lernprozess.
Der Lernprozess funktioniert folgendermaßen: Das Perzeptron gibt nur dann den Wert 1 aus, wenn die Summe des Produkts der gewichteten Eingänge größer ist als Theta. Wenn die Ausgabe in Bezug auf die Kombination der Eingänge korrekt ist, wird nichts verändert.
Wird jedoch ein Wert von 1 ausgegeben, obwohl eine 0 erforderlich wäre, so wird der Schwellwert Theta um eins erhöht. Im umgekehrten Fall, wenn also ein Wert von 0 ausgegeben wird, obwohl eine 1 erforderlich wäre, werden alle Gewichtungen, die mit den Eingängen von 1 verbunden sind, um 1 erhöht.
Der Gedanke hinter diesem Verfahren ist, dass nur die Eingänge mit einem Wert von 1 zu einer unerwünschten Ausgabe von 1 beitragen können, so dass es sinnvoll ist, deren Auswirkung zu reduzieren, indem die entsprechenden Gewichtungen verringert werden. Umgekehrt können nur Eingänge mit einem Wert von 1 zu einer gewünschten Ausgabe von 1 beitragen. Wenn die Ausgabe 0 und nicht wie gewünscht 1 ist, müssen die zugehörigen Gewichtungen erhöht werden.
Im Jahr 1958 wurde das Mark I Perzeptron als Hardware-Implementierung erstellt, nachdem es zunächst als Software auf einem IBM 704 realisiert worden war [4]. Angeschlossen an 400 Cadmiumsulfid-Fotozellen, die eine rudimentäre Kamera bildeten, und mit motorgesteuerten Potentiometern, die die Gewichtungen während des Lernens einstellten, konnte es nach dem Training die Form eines Dreiecks erkennen [5].
Das Problem der Perzeptronen
Obwohl dies bewies, dass ein elektronisches System potenziell lernen konnte, gab es ein entscheidendes Problem mit diesem Design: Es konnte nur linear trennbare Probleme lösen. Um auf die frühere McCulloch-Pitts-TLU zurückzukommen: Alle einfachen UND-, ODER-, NICHT-, NAND- und NOR-Funktionen sind linear trennbar. Das bedeutet, dass eine einzige Zeile die (in Bezug auf die Eingänge) gewünschten Ausgänge von den unerwünschten Ausgängen trennen kann (Bild 4). Anders verhält es sich bei XOR- (und den komplementären XNOR-) Funktionen. Wenn die Eingänge gleich sind (00 oder 11), ist der Ausgang 0, aber wenn die Eingänge unterschiedlich sind (01 oder 10), ist der Ausgang 1. Dies erfordert, dass der gewünschte Ausgang in Bezug auf die Eingänge in eine Gruppe eingeteilt wird. Vereinfacht ausgedrückt, kann das Perzeptron nicht trainiert werden, um zu lernen, wie XOR oder XNOR funktioniert, oder um seine Funktion zu replizieren.
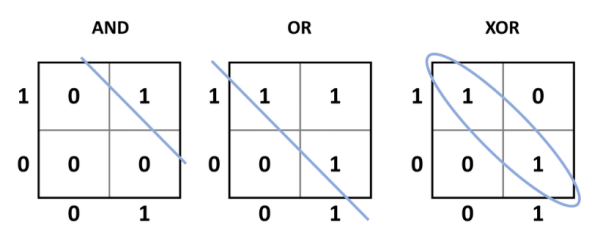
Bild 4. Von links nach rechts: AND-, OR- und XOR-Funktionen. Die 1-Ausgänge der ersten beiden können mit einer Geraden linear von den 0-Ausgangszuständen getrennt werden. Bei XOR ist das nicht möglich, so dass das Perzeptron es nicht lernen kann.
Das andere Hauptproblem lag in der verwendeten Aktivierungsfunktion. Die lineare Schwelleinheit machte einen scharfen Sprung zwischen inaktiv und aktiv. Die Forschungen, die zum Delta-Rule-Netzwerk [6] führten, zeigten, dass das Lernen durch Gradientenabstieg ein entscheidendes Element im Lernprozess eines neuronalen Netzwerks ist. Das bedeutete auch, dass jede Aktivierungsfunktion differenzierbar sein muss. Der plötzliche Sprung von 0 auf 1 in der linearen Schwelleneinheit ist aber am Übergangspunkt nicht differenzierbar (die Steigung wird unendlich), und der Rest der Funktion liefert einfach 0 (die Ausgabe bleibt unverändert).
Es wurde vorgeschlagen, das XOR-Problem mit einem Multilayer-Netzwerk mit mehreren versteckten Knoten zwischen den Eingangs- und Ausgangsknoten zu lösen. Außerdem könnte eine differenzierbare Funktion, etwa die logistische Funktion in Bild 5, eine Sigmoidkurve, eine stetige Aktivierungsfunktion liefern, die das Lernen mit Gradientenabstieg unterstützt. Die große Herausforderung war das Lernen - wie würden alle Gewichtungen trainiert werden?
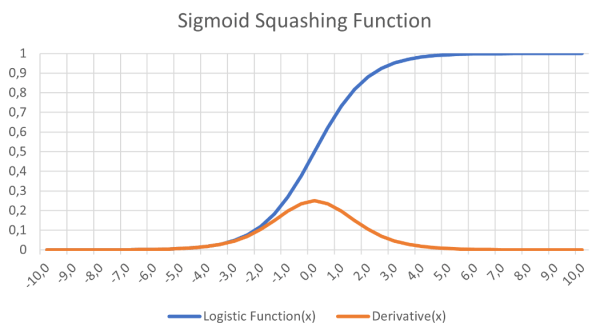
Dies hilft beim Lernen im Gradientenverfahren in neuronalen Netzen.
Der Delta-Rule-Ansatz hatte gezeigt, dass durch die Berechnung der quadratischen Abweichung des Netzes (gewünschte Ausgabe - tatsächliche Ausgabe) und die Implementierung einer Lernrate die Gewichtung im Netz sukzessive verbessert werden konnten, bis die optimalen Gewichtungsvektoren gefunden sind (Bild 6). Durch das Hinzufügen einer Schicht versteckter Knoten zwischen Ein- und Ausgang wurde die Berechnung zwar komplizierter, aber nicht unmöglich, wie wir sehen werden.
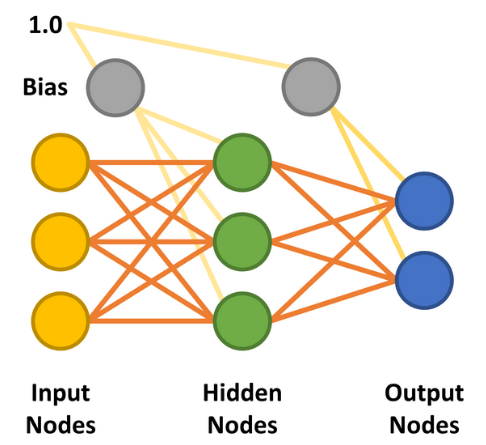
Multilayer-Perzeptron
Das Multilayer-Perzeptron (MLP) wurde durch das Hinzufügen der versteckten Schicht möglich. Die einfachste Form eines neuronalen Netzes mit MLP verwendet nur eine einzige versteckte Schicht. Alle Knoten sind miteinander verbunden (fully connected), wobei zwischen jedem Eingangknoten und verstecktem Knoten sowie zwischen jedem versteckten Knoten und Ausgangsknoten Gewichtungen zugewiesen sind. Die Linien zwischen den Knoten stellen die Gewichtungen dar. Die gewünschten Eingaben werden an die Eingangsknoten angelegt (Werte zwischen 0,0 und 1,0) und das Netzwerk berechnet die Antwort jedes versteckten Knotens und Ausgangsknotens - ein Schritt, der als Feedforward-Phase bezeichnet wird. Dies sollte ein Ergebnis liefern, das zeigt, dass die Eingangswerte mit einer Ausgangskategorie übereinstimmen, die das Netzwerk erlernt hat.
Die Eingänge könnten zum Beispiel mit einer 28 × 28 Pixel großen Kamera verbunden sein, die auf handgeschriebene Zahlen gerichtet ist. Die MNIST-Datenbank mit handgeschriebenen Ziffern, die genau solche Bildgrößen enthält, könnte die Trainingsmenge bilden [7]. Jeder der Ausgänge würde eine der Zahlen von 0 bis 9 repräsentieren. Wenn die Zahl 7 vor die Kamera gehalten wird, würde jeder Ausgang die Wahrscheinlichkeit angeben, dass die Eingabe dieser Zahl 7 entspricht. Der Ausgang 0 zeigt (hoffentlich) an, dass die handgeschriebene Zahl völlig unwahrscheinlich eine 0 ist, wie auch die acht anderen Ausgänge. Lediglich der Ausgang 7 sollte eine hohe Wahrscheinlichkeit anzeigen, dass die handgeschriebene Zahl eine 7 ist. Einmal trainiert, sollte dies die erwartete Funktionalität für eine 7 aus dem Trainingsdatensatz oder einer neu handgeschriebenen 7 sein, die von einem Menschen erkannt werden kann.
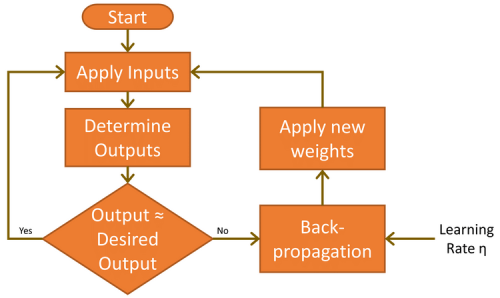
Bevor dies geschieht, muss das Netzwerk die vorliegende Aufgabe lernen. Dies wird erreicht, indem der Input (handgeschriebene Siebenen) angelegt und die Ergebnisse, die die Ausgänge liefern, analysiert werden. Da diese anfangs wahrscheinlich nicht korrekt sind, wird ein Lernzyklus durchgeführt, um die Gewichtungen so zu verändern, dass der Fehler reduziert wird. Dieser iterative Lernprozess, bekannt als Backpropagation, wird viele tausend Mal ausgeführt, bis die Genauigkeit des Netzwerks den Anforderungen der Anwendung entspricht (Bild 7). In der Welt des ML wird dies als supervised learning, überwachtes Lernen bezeichnet.
Es gibt zwei weitere wichtige Faktoren, die in der Feedforward- und Backpropagation-Phase berücksichtigt werden müssen. Der erste ist der Bias. Ein Bias-Wert von 1,0 multipliziert mit einer Gewichtung (zwischen 0,0 und 1,0) wird während der Feedforward-Phase auf die Knoten der versteckten und der Ausgabeschicht angewendet. Die Aufgabe des Bias ist es, die Problemlösungsfähigkeiten des Netzwerks zu verbessern und im Wesentlichen die logistische Aktivierungsfunktion (siehe wieder Bild 5) nach links oder rechts zu verschieben. Der andere Wert ist die Lernrate, wiederum ein Wert zwischen 0,0 und 1,0, die bestimmt, wie schnell das MLP lernt, das gegebene Problem zu lösen, auch bekannt als die Geschwindigkeit der Konvergenz. Wenn dieser Wert zu niedrig eingestellt ist, löst das Netzwerk das Problem mit einer angemessenen Genauigkeit möglicherweise nie, ist der Wert zu hoch, läuft das Netzwerk Gefahr, während des Lernens zu oszillieren und ebenfalls kein ausreichend genaues Ergebnis zu liefern (siehe auch Grenzen des Gradientenlernens).
Das hier beschriebene MLP könnte als „Vanilla-Entwurf“ betrachtet werden. Neuronale Netze können jedoch auf eine Vielzahl von Arten implementiert werden. Dazu gehören mehr als eine versteckte Schicht, eine nicht vollständige Verbindung der Knoten, die Verknüpfung späterer mit früheren Knoten und die Verwendung unterschiedlicher Aktivierungsfunktionen [8].
Es gibt Zeiten, in denen das neuronale Netz scheinbar nicht in der Lage ist, zu lernen, obwohl es zuvor die erforderliche Funktionalität mit der gleichen Knotenkonfiguration gelernt hat. Dies kann darauf zurückzuführen sein, dass das Netz in einem relativen Minimum stecken bleibt, anstatt ein absolutes Minimum der Fehlerfunktion zu finden.
MLP in Aktion
Das Prinzip ist hoffentlich klar, son dass wir ein konkretes Beispiel untersuchen können. Das Beispiel stammt aus einem hervorragenden Artikel von Matt Mazur, der sich viel Zeit genommen hat, um die Backpropagation in einem MLP mit nur einer einzigen versteckten Schicht zu erklären [9]. Das Beispiel besitzt ein hohen Niveau, aber diejenigen, die an mehr Details interessiert sind (und keine Angst vor Mathematik haben), sollten Matts Artikel studieren. Sobald das mathematische Prinzip des Beispiels verstanden ist, können wir eine Software-MLP-Implementierung betrachten, die mit den gleichen Parametern wie in dieser theoretischen Analyse arbeitet. Wenn Sie mitmachen wollen; es gibt es eine Excel-Tabelle, die zu Matts Beispiel passt. Laden Sie einfach das Repository von GitHub [10] herunter oder klonen Sie es und werfen Sie einen Blick auf workedexample/Matt Mazur Example.xlsx im Ordner.
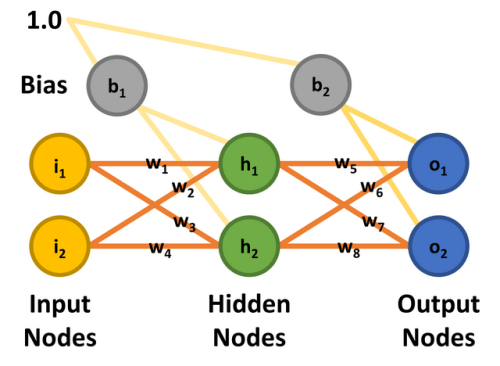
Der Einfachheit halber wird ein MLP mit zwei Eingängen, zwei Ausgängen und zwei versteckten Knoten verwendet. Die Eingangsknoten werden mit i1 und i2 bezeichnet, die versteckten Knoten h1 und h2 und die Ausgangsknoten o1 und o2. Ziel der Übung ist, das Netzwerk so zu trainieren, dass es am Knoten o1 0,01 und am Knoten o2 0,99 ausgibt, wenn der Knoten i1 0,05 und i2 0,10 ist. Es gibt acht Gewichtungen (w1 bis w8) und zwei Bias-Werte (b1 und b2). Damit die Mathematik durchgerechnet werden kann, sind allen Eingangsknoten, Bias‘ und Gewichtungen die in Bild 8 gezeigten Werte zugewiesen und stimmen mit dem Artikel von Matt Mazur überein.
Feedforward
In der Feedforward-Phase zur Berechnung der Ausgänge o1 und o2 erhält jeder versteckte Knoten einen Eingang, der die Summe der Eingänge multipliziert mit den Gewichtungen ist, zuzüglich des Biaseingangs (b1 = 0,35). Im Prozess und mit den Gleichungen von Matt Mazur ist der Eingang für h1 die Summe von i1 multipliziert mit w1 (0,15), i2 multipliziert mit w2 (0,20) und b1 (0,35).
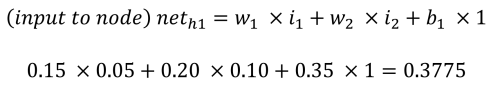
Der Ausgangswert jedes versteckten Knotens wird durch die logistische (Aktivierungs-) Funktion bestimmt, die den Ausgang des versteckten Knotens auf einen Wert zwischen 0,0 und 1,0 drückt. Dies wird wie folgt berechnet:
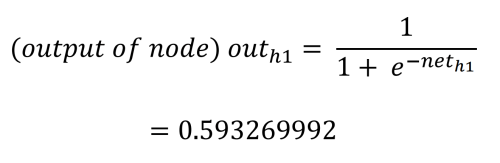
Wiederholt man den Vorgang für h2 (mit w3 = 0,25, w4 = 0,3 und b1 = 0,35), erhält man:
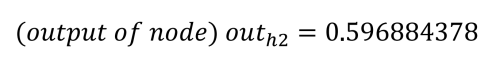
Die Netzeingänge zu den Ausgangsknoten werden auf die gleiche Weise berechnet, wobei die berechneten Ausgangswerte der versteckten Knoten verwendet und die Gewichte 5 bis 8 (w5 = 0,4, w6 = 0,45, w7 = 0,5 und w8 = 0,55) sowie der Bias-Wert b2 = 0,60 eingesetzt werden.
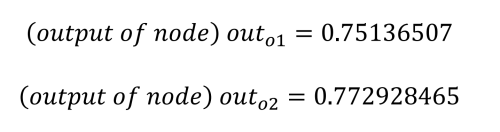
Wie bereits erwähnt, ist es unser Ziel, dass o1 einen Wert von 0,01 und o2 einen Wert von 0,99 ausgibt, aber wir sehen, dass wir von diesem Ergebnis noch ein Stück entfernt sind. Der nächste Schritt ist deshalb die Berechnung des Fehlers in jedem Ausgang mit Hilfe der quadratischen Fehlerfunktion.
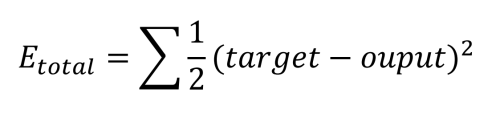
Dieser wird für jeden Ausgang wie folgt berechnet:
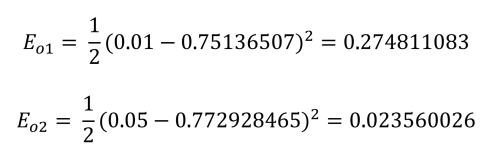
Schließlich kann der Gesamtfehler für das Netzwerk ermittelt werden:
Der nächste Schritt ist, herauszufinden, wie man diesen Fehler verbessern kann.
Backpropagation
Bei der Backpropagation findet das eigentliche „Lernen“ statt. Der Prozess umfasst die Bestimmung des Beitrags, den jede Gewichtung zum Gesamtfehler leistet. Es beginnt mit der Betrachtung der Gewichte zwischen den versteckten Knoten und den Ausgangsknoten. Was die Sache verkompliziert, ist, dass w5 zum Gesamtfehler über die zwei Ausgangsknoten o1 und o2 beiträgt, die aber auch von den Gewichten w6 bis w8 beeinflusst werden. Es sollte auch beachtet werden, dass die Bias-Werte bei diesen Berechnungen keine Rolle spielen.
Die dazu erforderliche Mathematik ist recht komplex, aber sie reduziert sich endlich auf einige einfache Multiplikationen, Additionen und Subtraktionen. Die Berechnung des neuen Wertes für w5 unter Berücksichtigung der gewählten Lernrate η (0,5) wird wie folgt durchgeführt:
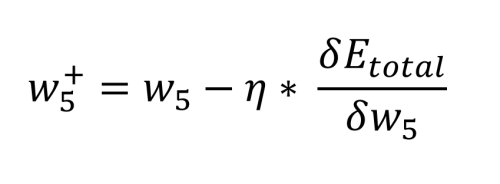
Danach können wir die alten Gewichtungen überprüfen und mit den neuen Gewichten für w5 bis w8 vergleichen:

Schon bei einer kurzen Überprüfung sehen wir, dass dies sinnvoll ist. Wir wollen, dass o1 durch w5 und w6 nach unten in Richtung 0,01 und o2 durch w7 und w8 nach oben in Richtung 0,99 gedrückt wird.
Der letzte Schritt besteht darin, den Einfluss zu bestimmen, den die Gewichte zwischen den Eingängen und den versteckten Knoten auf den Fehler am Ausgang ausüben. Wieder reduziert sich die Mathematik auf die Grundrechenarten, und tatsächlich sieht die Gleichung genauso aus wie die, die zur Berechnung der neuen Gewichtungen w5 bis w8 verwendet wurde. Der Unterschied besteht darin, wie der Gesamtfehler in Bezug auf die Gewichtung (ursprünglich w1) berechnet wird, da die Ausgabe der versteckten Schicht von einer anderen Eingabe und einer anderen Gewichtung abhängig ist (für h1, i1 und w1 sowie i2 und w2):
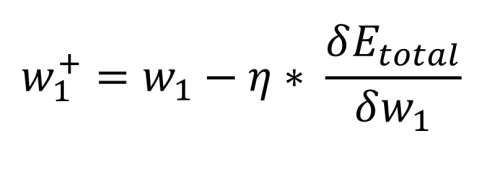
Auch bei dieser Berechnung spielt der Bias-Wert keine Rolle. Nun können wir die alten Gewichte w1 bis w4 und die neuen Gewichte vergleichen:

Die alten Gewichtungen werden von den ermittelten neuen Gewichtungen ersetzt und ein neuer Vorwärtsdurchlauf durchgeführt. Solange der Ausgangsfehler größer als gewünscht bleibt, können die beschriebenen Backpropagation-Durchläufe wie hier beschrieben wiederholt werden.
MLP-Implementierung in Processing
Um dieses einfache neuronale Netzwerk zu demonstrieren, wurde ein neuronales Netzwerk von Grund auf als Klasse kodiert, die in der Entwicklungsumgebung Processing [11] (die speziell für das Kodieren in der visuellen Kunst entwickelt wurde) verwendet werden kann. Diese visuellen Fähigkeiten erlauben der IDE die einfache Darstellung von 2D- und 3D-Grafiken. Durch die Ausgabe auf eine Textkonsole können zudem Ideen schnell und einfach getestet werden. Der folgende Code ist Teil des erwähnten Repositorys [10].
Der Code für die MLP-Implementierung befindet sich im Ordner processing/neural/neural.pde. Diese Datei wird einfach zu jedem Ihrer Processing-Projekt hinzugefügt. Die Klasse Neural kann instanziiert werden, um eine beliebige Anzahl von Eingabe-, versteckten und Ausgabeknoten zu unterstützen. Um das obige Beispiel nachzuvollziehen, sollte nun die Datei processing/nn_test/nn_test.pde in Processing geöffnet werden.
Das Erstellen eines neuronalen Netzwerks ist recht einfach. Zunächst wird der Klassenkonstruktor Neural (in nn_test.pde) aufgerufen, um ein Objekt mit (hier) dem Namen network zu erstellen, das die gewünschte Anzahl von Eingängen, versteckten Knoten und Ausgängen (2, 2 und 2) definiert. Nach der Erstellung werden weitere Member-Funktionen aufgerufen, um die Lernrate und die Biaswerte für den versteckten und den Ausgangsknoten gemäß der Beispielskizze einzustellen.
Der Konstruktor initialisiert auch die Gewichtungen mit Zufallswerten zwischen 0,25 und 0,75. Für das obige Beispiel ändern wir die Gewichtungen wie in Listing 1 gezeigt, wo auch die Eingangswerte und die gewünschten Ausgangswerte definiert sind.

Der Beispielcode aktiviert auch einen Verbose-Modus, in dem die Arbeit für jeden Schritt der Berechnungen angezeigt wird. Diese sollten mit den Ergebnissen in der Excel-Tabelle übereinstimmen. Nach einem Klick auf Run in Processing sollte die Textkonsole folgendes ausgeben:
...forwardpass complete. Results:
For i1 = 0.05 and i2 = 0.1
o1 = 0.75136507 (but we want: 0.01 )
o2 = 0.7729285 (but we want: 0.99 )
Total network error is: 0.2983711
Danach wird learning aktiviert und wieder ein Vorwärtsdurchlauf ausgeführt, gefolgt von dem Backpropagation-Schritt. Dies führt zur Ausgabe der neuen und alten Gewichte und zur Berechnung eines neuen Vorwärtsdurchlaufs, um die neuen Ausgangsknotenwerte und Fehler zu bestimmen:
New Hidden-To-Output Weight [ 0 ][ 0 ] = 0.3589165, Old Weight = 0.4
New Hidden-To-Output Weight [ 1 ][ 0 ] = 0.40866616, Old Weight = 0.45
New Hidden-To-Output Weight [ 0 ][ 1 ] = 0.5113013, Old Weight = 0.5
New Hidden-To-Output Weight [ 1 ][ 1 ] = 0.56137013, Old Weight = 0.55
New Input-To-Hidden Weight[ 0 ][ 0 ] = 0.14978072, Old Weight = 0.15
New Input-To-Hidden Weight[ 1 ][ 0 ] = 0.19956143, Old Weight = 0.2
New Input-To-Hidden Weight[ 0 ][ 1 ] = 0.24975115, Old Weight = 0.25
New Input-To-Hidden Weight[ 1 ][ 1 ] = 0.2995023, Old Weight = 0.3
Wir können sehen, dass dies die Gewichtungen 5 bis 8 und dann 1 bis 4 darstellt. Sie stimmen auch mit den zuvor durchgeführten Überschlagsberechnungen überein (mit kleinen Abweichungen aufgrund von Rundungsfehlern).
Nächste Schritte mit MLP
Nachdem Sie ein gutes Verständnis für die Funktionsweise eines neuronalen MLP-Netzes und für die hier zur Verarbeitung bereitgestellte beispielhafte Neuronalklasse entwickelt haben, haben Sie eine gute Ausgangsposition, um selbständig weitere Experimente durchzuführen. Hier einige Ideen:
- Ausführen des Lernens in einer Schleife - wie viele Durchläufe sind erforderlich, um einen Netzwerkfehler von 0,001, 0,0005 oder 0,0001 zu erreichen?
- Spielen Sie mit unterschiedlichen Biaswerten und Gewichtungen - wie wirkt sich dies auf die Anzahl der zum Lernen erforderlichen Durchläufe aus? Scheitert das neuronale Netzwerk irgendwann beim Lernen?
- Ordnen Sie die Ausgaben den Eingaben zu – und versuchen Sie, eine 3D-Darstellung jeder Ausgabe gegen die Eingaben zu entwickeln, sobald das Netzwerk seine Aufgabe gelernt hat. Sieht es so aus, wie Sie es erwarten würden? Probieren Sie auch mal das Chart-Studio von Plotly [12] aus, anstatt eine Tabellenkalkulation zum Plotten der Ausgabedaten zu verwenden.
Im nächsten Teil dieser Artikelreihe werden wir unserem neuronalen Netzwerk beibringen, wie man Logikgatter implementiert und seinen Lernprozess visualisiert.
Haben Sie Fragen oder Kommentare zu diesem Artikel? Dann schreiben Sie dem Autor eine E-Mail an stuart.cording@elektor.com.


Diskussion (4 Kommentare)