Präzise, richtig oder genau? Ihre Messgeräte müssen alles sein!

Beim Verfassen technischer Fachartikel läuft man leicht Gefahr, sprachlich ungenau zu werden – besonders in strengen Disziplinen wie der Messtechnik, in denen jeder Begriff eine klar definierte Bedeutung hat und unsaubere Terminologie in der Regel wenig geschätzt wird.

Messungen

Eine Messung ist per Definition eine zahlenmäßige Beziehung, die sich aus dem Vergleich einer gegebenen Größe mit einer anderen, gleichartigen und bekannten Größe ergibt, die als Referenz betrachtet wird.

Unabhängig von der verwendeten Einheit können weder der Vergleich noch die darauf basierenden Berechnungen völlig fehlerfrei sein: Messfehler sind unvermeidlich! Sie lassen sich zwar reduzieren, aber nie vollständig ausschließen. Im technischen und wissenschaftlichen Umfeld besteht der richtige Umgang mit Messfehlern darin, das Ausmaß dieser Fehler zu quantifizieren und sie systematisch in den Messprozess einzubeziehen.

In der Mess- und Prüftechnik gilt grundsätzlich: Qualität hat ihren Preis. Hochwertige, meist teure Messgeräte können die Messunsicherheit deutlich verringern und damit die Aussagekraft und Zuverlässigkeit der Ergebnisse steigern. Vor der Anschaffung eines Messgeräts sollten Techniker und Ingenieure daher genau prüfen, welches Qualitätsniveau ein Gerät bietet und dabei gegebenenfalls einen bewussten Kompromiss zwischen Preis und Leistung eingehen.

Begriffe wie Präzision, Genauigkeit, Richtigkeit, Wiederholbarkeit, Langzeitstabilität, Empfindlichkeit, Auflösung, Betriebsbereitschaft und Vollbereichswert sind inzwischen geläufig und können die Auswahl aus dem breiten Angebot handelsüblicher Geräte erleichtern. In diesem Zusammenhang jedoch geraten drei Begriffe besonders häufig ins Kreuzfeuer: Präzision, Richtigkeit und Genauigkeit, die oft synonym und unsachgemäß verwendet werden (was allerdings nicht zwangsläufig gravierende Folgen hat).

Eine erste Definition

Was bedeuten Genauigkeit, Richtigkeit und Präzision in der Messtechnik wirklich? Beginnen wir mit drei prägnanten Definitionen:

• Präzision: Ein Messgerät gilt als präzise, wenn es Messwerte erzeugt, die möglichst eng um den Mittelwert der aufgenommenen Messreihe streuen.
• Richtigkeit: Die Richtigkeit beschreibt die Differenz des Mittelwerts der Messwerte vom tatsächlichen, wahren Wert.
• Genauigkeit: Ein Messgerät gilt als genau, wenn es Messwerte liefern kann, die möglichst eng und nahe am Referenz- beziehungsweise wahren Wert liegen, also präzise und richtig sind.

Nach dieser kurzen Begriffsbestimmung ist ein wichtiger Punkt hervorzuheben: Bei nur einer einzigen Messung lässt sich - wenn auch nur näherungsweise – die Richtigkeit eines Messgeräts beurteilen, jedoch nicht seine Präzision. Für eine Aussage über die Präzision ist eine ausreichende Anzahl von Messwerten erforderlich, sodass statistisch relevante Aussagen getroffen werden können. Bevor es weiter ins Detail geht, ist es sinnvoll, zunächst den Begriff des Messfehlers näher zu betrachten.

Messfehler

Bei einer Einzelmessung wird der Fehler als die Differenz zwischen dem gemessenen Wert X und dem wahren Wert θ beziehungsweise einem als wahr angenommenen Referenzwert der betreffenden Messgröße definiert. Man spricht in diesem Fall vom absoluten Fehler, mit η = X − θ.

Der absolute Fehler allein hat jedoch nur begrenzte Aussagekraft, da er keine Information über das Verhältnis des Fehlers zur Größe der Messgröße liefert. Aus diesem Grund wird die Fehlergröße häufig als Verhältnis des absoluten Fehlers η zum wahren Wert θ angegeben – der sogenannte relative Fehler ε = η / θ.

Ein relativer Fehler lässt sich nur berechnen, wenn der Referenzwert θ bekannt ist. In der Praxis wird ε meist als Prozentwert angegeben, indem er mit 100 multipliziert wird. Daher wird der prozentuale Fehler in der Regel für jeden Messbereich eines Messgeräts separat ausgewiesen.

Fehlerarten

Fehler bei experimentellen Messungen können zahlreiche Ursachen haben – darunter auch Verfahrens- oder Bedienfehler. Besonders bei analogen Messgeräten spielt der Einfluss des Anwenders eine größere Rolle, wie im Kasten Analog- oder Digitalanzeige? Die Auflösung zählt! näher erläutert wird.

Im Folgenden gehen wir jedoch davon aus, dass keine Bedienfehler vorliegen und dass alle auftretenden Fehler im Wesentlichen auf zufällige Einflüsse und gerätespezifische Eigenschaften zurückzuführen sind.

Grundsätzlich lassen sich Messfehler in zwei Hauptkategorien einteilen:

• Systematische Fehler, die Messwerte stets in eine bestimmte Richtung verschieben. Diese Fehlerart kann in vielen Fällen verringert oder sogar ganz beseitigt werden. Sie wirkt sich primär auf die Richtigkeit eines Messgeräts aus.
• Zufällige Fehler, die durch technische Eigenschaften des Geräts, die Qualität von Entwurf und Bauteilen sowie durch unvorhersehbare und/oder nicht kontrollierbare Einflüsse während der Messung entstehen. Diese Fehlerart beeinträchtigt vor allem die Präzision eines Geräts. Sie lässt sich nicht vollständig eliminieren, kann aber durch Wiederholung der Messung und anschließende statistische Auswertung zumindest abgeschätzt werden.

Bei elektronischen Messgeräten können systematische Fehler beispielsweise durch langfristige Veränderungen der Bauteileigenschaften (Alterung oder Derating) oder durch kurzfristige Abweichungen wie eine Überschreitung des zulässigen Betriebstemperaturbereichs entstehen. Hochwertigere Geräte verfügen in der Regel über eine oder mehrere entweder hardware- oder softwarebasierte Kalibrierfunktionen, mit denen sich diese Fehler weitgehend kompensieren lassen.

Zufällige Fehler hingegen können etwa durch elektromagnetische Störeinflüsse (EMI) entstehen, die über Messleitungen eingekoppelt werden, oder durch instabile oder minderwertige Signalaufbereitung beziehungsweise Abtastung im Frontend. Solche Fehler lassen sich teilweise durch Abschirmmaßnahmen reduzieren. Liegen die Ursachen jedoch in einem grundlegend mangelhaften Entwurf oder anderen konstruktiven Schwächen, sind sie durch äußere Maßnahmen kaum zu beheben.
 

Analog- oder Digitalanzeige? Die Auflösung zählt!

Die Auflösung eines Messgeräts ist die kleinste Änderung der Messgröße, die das Gerät zuverlässig erfassen und anzeigen kann.

Im gezeigten Beispiel sind ein analoges Milliamperemeter von Cassinelli & C. (von etwa 1960) und ein digitales High-End-Multimeter vom Typ Siglent SDM3055 (Modelljahr 2024) in Reihe an eine Stromquelle mit 30 mA angeschlossen. Das obere Bild zeigt die Skala 0…50 mA des analogen Instruments, dessen Genauigkeit übrigens auch nach über 60 Jahren noch bemerkenswert ist! Die Skala ist mit großen Teilstrichen zu je 1 mA und kleineren zu je 0,5 mA unterteilt, woraus sich eine Auflösung von 0,5 mA (entsprechend 500 µA) ergibt.

Der kritische Punkt bei analogen Anzeigen liegt in der optischen Einschätzung der Zeigerposition zwischen zwei Teilstrichen – eine Bewertung, die zwangsläufig subjektiv ist und stark von der jeweiligen Person abhängt.

Beim digitalen Gerät zeigt das Display einen Wert von 29,690 mA auf fünf Stellen an. Die letzte Ziffer steht für die kleinste darstellbare Einheit, also 0,001 mA (entspricht 1 µA). Selbstverständlich erlaubt die Auflösung allein keinerlei Rückschlüsse auf die Richtigkeit oder Präzision eines Instruments! 

Ein erstes Praxisbeispiel

Nehmen wir an, im Labor befinden sich vier Multimeter, deren Zuverlässigkeit überprüft werden sollen möchten. Für einen ersten Funktionstest (Go-/No-Go-Test) steht eine hochpräzise Referenzstromquelle zur Verfügung, der entsprechend vorbereitet wird.

Für den Test wird die Stromquelle auf exakt 2,000 A eingestellt. Dieser Wert wird als wahrer Wert, Referenzwert oder θ betrachtet. Angenommen, das erste (und einzige) Messergebnis des überprüften Multimeters, im Folgenden als Messwert oder X bezeichnet, beträgt 2,0052 A. Daraus ergibt sich, wie bereits erläutert, ein absoluter Fehler:

η = X − θ

η = 2,0052 - 2,0000 = 0,0052 A

Aus dem bekannten absoluten Fehler η lässt sich der relative Fehler ε berechnen. Ausgedrückt in Prozent ergibt sich:

ε = (η / θ) × 100

ε = (0,0052 / 2,0000) × 100 = 0,26%

Dieser Wert ist eine dimensionslose Zahl (ohne physikalische Einheit) und bedeutet, dass das Multimeter in dieser konkreten Messung und in dem gewählten Bereich einen relativen Fehler von 0,26 % aufweist.

Statistische Auswertung

Die einzelne Messung, die wir bislang mit dem ersten unserer Multimeter durchgeführt haben, erlaubt keine verlässliche Aussage über die Gesamtzuverlässigkeit des Geräts. Ebenso wenig lässt sich daraus ableiten, ob systematische, zufällige oder kombinierte Fehler vorliegen. Für eine fundiertere Analyse erweitern wir daher den Ansatz und erstellen vier Messdatenbanken – jeweils eine für jedes Multimeter.

Dazu führen wir an jedem Gerät je 100 aufeinanderfolgende Messungen durch. Dabei achten wir darauf, die Prüfbedingungen zwischen den einzelnen Messungen konstant zu halten. Jeder Messwert wird als X_n bezeichnet.

Aus diesen Daten berechnen wir anschließend den arithmetischen Mittelwert der jeweiligen Messreihe. Dieser wird als mittlerer Messwert µ definiert (mit n = 100 in unserem Fall):

µ = (X₁ + X₂ + X₃ … + X_n) / n 

Der Mittelwert µ erlaubt erste Rückschlüsse auf die durchschnittliche Richtigkeit des Geräts. Er genügt jedoch nicht, um den zufälligen Anteil des Messfehlers, also die Präzision, zu bewerten.

Deshalb berechnet man auf Basis derselben Daten für jede der vier Messreihen zusätzlich die Standardabweichung σ. Dabei wird davon ausgegangen, dass die Verteilung der Messwerte der Normalverteilung folgt. Die Standardabweichung σ der Messwerte X₁…X₁₀₀ wird mit folgender Formel ermittelt:

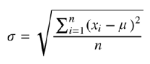
Auf diese Weise lässt sich beurteilen, wie stark die einzelnen Messwerte vom zuvor bestimmten Mittelwert abweichen.

Wenn Ihnen das Konzept der Standardabweichung nicht vertraut ist, hilft ein Blick in Quelle weiter. Eine genauere, mathematische Erklärung finden Sie in Quelle. Zusätzlich bietet der Textkasten Gaußsche Glockenkurve, in Kürze einen kurzen Überblick.

Gaußsche Glockenkurve, in Kürze

In der Wissenschaft entstehen viele bedeutende Entdeckungen durch das Zusammenwirken mehrerer Forscher. So verhält es sich auch mit der Gaußschen Normalverteilung. Ihr Konzept entwickelte sich aus verschiedenen Beobachtungen, beginnend Ende des 18. Jahrhunderts mit dem zentralen Grenzwertsatz von Laplace.

Abraham de Moivre erkannte anschließend, dass sich mit zunehmender Anzahl von Ereignissen eine zunehmend geglättete Verteilung ergibt. Schließlich war es Carl Friedrich Gauß, der die mathematische Formel zur Berechnung der Kurve definierte, die später seinen Namen erhielt. Eine interessante historische Zusammenfassung dieser Forschung, die die Grundlage der modernen Statistik bildet, ist unter zu finden.

Bild A zeigt eine typische Gaußsche Glockenkurve. In einer Normalverteilung treten Werte in einer Stichprobe mit größerer Häufigkeit auf, je näher sie am Mittelwert µ liegen, dem arithmetischen Mittel aller Daten.

Diese Häufung verleiht der Kurve ihre charakteristische glockenförmige Form. Die Fläche unter der Kurve stellt die Verteilung der Messdaten dar. Die Y-Achse zeigt, wie oft ein bestimmter Wert in der Stichprobe vorkommt.

Der Abstand zwischen dem Mittelwert µ und dem Wendepunkt der Kurve, also dem Punkt, an dem sich die Krümmung umkehrt, entspricht der sogenannten Standardabweichung oder Sigma (σ). Weitere gebräuchliche Begriffe sind Wurzel der mittleren quadratischen Abweichung (root-mean-square deviation, RMSD) oder Wurzel des mittleren quadratischen Fehlers (root-mean-square error, RMSE).

Anders ausgedrückt: Sigma (σ) kann als Maß für die Streuung der Daten um den Mittelwert µ betrachtet werden. Sigma und Präzision verhalten sich umgekehrt proportional – je geringer die Streuung (also je kleiner σ), desto höher die Präzision. Die Gaußkurve wird dann entsprechend schmaler und spitzer. Umgekehrt führt ein hoher Sigma-Wert zu einer abgeflachten Kurve mit breiter Basis.

Eine in der Praxis häufig verwendete Faustregel für die Normalverteilung besagt: Etwa 68,26 % aller Messwerte liegen im Intervall [–σ … +σ] (blauer Bereich in Bild A). Rund 95,44 % fallen in den erweiterten Bereich [–2σ … +2σ] (blauer und violetter Bereich), und ganze 99,73 % der Werte befinden sich im Bereich [–3σ … +3σ], also innerhalb des blauen, violetten und grünen Bereichs.

Sigma ist keine dimensionslose Größe, sondern übernimmt die Einheit der betrachteten Messgröße, im Fall unseres Multimeter-Beispiels also Ampere (A).

Interpretation der Daten

Multimeter 1

Aus den hundert Messungen mit Multimeter 1 wurden der Mittelwert µ sowie die Standardabweichung σ gemäß der vorher beschriebenen Methode berechnet. Die resultierende Verteilung ist in Bild 1 dargestellt. Die Kurve zeigt eine Normalverteilung der Messwerte um den Mittelwert µ, der in diesem Fall bei µ = 1,9 A liegt. Die Verteilung ist stark gebündelt, was auf eine hohe Konzentration der Messwerte nahe am Mittelwert hinweist – ein Zeichen für gute Präzision. Allerdings liegt dieser Mittelwert deutlich unter dem wahren Wert θ = 2 A. Die Differenz δ = (µ − θ) = −0,1 A steht für die systematische Abweichung, also die durchschnittliche Unrichtigkeit dieses Geräts.

Dies ist ein typischer Fall, bei dem eine Kalibrierung helfen kann, den systematischen Fehleranteil deutlich zu reduzieren,  δ auf nahezu null zu bringen und damit die erwartete Genauigkeit wiederherzustellen.

Der Abstand zwischen den extremsten Messwerten (angezeigt durch den roten Doppelpfeil an der Basis der Glockenkurve) stellt die maximale Messunsicherheit dar. In der Messtechnik gilt: Je höher die Präzision, desto geringer die Unsicherheit – und umgekehrt.

Mit einer Standardabweichung von σ = 0,042 A (das entspricht einem Standardfehler von ±2,2 % relativ zum Mittelwert µ) kann festgehalten werden: Das Gerät arbeitet präzise, ist jedoch aufgrund des hohen systematischen Fehlers (δ = −0,1 A) unrichtig – der durchschnittliche Messfehler beträgt −5 % zum Referenzwert.

Multimeter 2

Das Diagramm zu Multimeter 2 (Bild 2) zeigt ein grundlegend anderes Bild. Der Mittelwert der Messreihe beträgt µ = 1,998 A, liegt also sehr nahe am Referenzwert. Dennoch ist die maximale Messunsicherheit dieses Geräts deutlich größer als bei Multimeter 1.

Mit einer Standardabweichung von σ = ±0,116 A (entsprechend ±5,8 % Fehler relativ zum Mittelwert) weist das Gerät einen erheblichen zufälligen Fehleranteil auf. Die Messwerte sind stark streuend und nicht um den Mittelwert konzentriert. Da sich dieser Zufallsfehler nicht vollständig kompensieren lässt, führt er zu einer geringen Präzision – auch wenn die scheinbar beeindruckende Richtigkeit von δ = −0,012 A (−0,6 % Fehler zum Referenzwert) etwas anderes suggerieren könnte.

Insgesamt handelt es sich um ein Gerät mit hoher Richtigkeit, aber sehr geringer Präzision – und somit für den Laboreinsatz ungeeignet, da die Wahrscheinlichkeit für unzuverlässige oder unrealistische Messergebnisse hoch ist. In einer anderen, aber gebräuchlichen Terminologie lässt sich sagen: Dieses Multimeter besitzt eine sehr geringe Wiederholgenauigkeit, ein direkter Ausdruck mangelnder Präzision.

Dieses Beispiel zeigt deutlich, dass Richtigkeit allein nicht ausreicht, um eine verlässliche Messung sicherzustellen.

Multimeter 3

Die Situation bei Multimeter 3 ist noch ungünstiger – falls das überhaupt möglich ist. Das Diagramm in Bild 3 zeigt einen berechneten Mittelwert von µ = 2,15 A mit einer systematischen Abweichung δ = 0,15 A, was einem Fehler von +7,5 % relativ zum Referenzwert entspricht. Dieser Wert allein ist bereits als signifikant schlecht zu betrachten. Darüber hinaus beträgt die Standardabweichung σ = ±0,19 A, entsprechend einem Fehler von ±8,8 % bezogen auf den Mittelwert µ. Die resultierende Verteilungskurve ist extrem abgeflacht, was auf einen sehr ausgeprägten zufälligen Fehler hinweist. Die Gesamtabweichung ist so groß, dass sie im Diagramm über den rechten Rand hinausgeht. Daher ist dieses dritte Gerät sowohl grob unpräzise als auch ungenau.

Multimeter 4

Die Kurve des vierten Messgeräts (Bild 4) stellt das beste Ergebnis der gesamten Serie dar. Die Fehlerverteilung ist eng um den Mittelwert µ = 2,006 A konzentriert. Die daraus resultierende systematische Abweichung δ = 0,006 A (entsprechend einem Fehler von +0,3 % relativ zum Referenzwert) ist als vernachlässigbar einzustufen. Auch die Standardabweichung beträgt lediglich σ = ±0,04 A (±2 % des Mittelwerts), was auf eine geringe Streuung hinweist. Daraus lässt sich eindeutig schließen, dass es sich um ein sowohl präzises Messgerät handelt, das richtige Ergebnisse liefert. Aufgrund dieser Eigenschaften kann es als genau bezeichnet werden.

Eine anschaulichere Darstellung

Für eine praxisnähere Veranschaulichung kann die Übersicht in Bild 5 hilfreich sein. Darin sind die Messwertverteilungen der zuvor beschriebenen Beispiele als Trefferbilder auf vier Zielscheiben dargestellt. Dieses Darstellungsformat ist in solchen Fällen weit verbreitet, da es sich besonders intuitiv interpretieren lässt. Zusätzlich markieren grüne und blaue Umrahmungen die Bereiche der systematischen beziehungsweise der zufälligen Fehleranteile. Im ungünstigsten Fall von Multimeter 3 überlagern sich diese Bereiche deutlich, da hier sowohl der systematische als auch der zufällige Fehleranteil sehr hoch ausfällt.

Idealtypisch ließen sich in dieser Darstellung kartesische Koordinaten überlagern, wobei die Y-Achse die Präzision und die X-Achse die Richtigkeit beschreibt. Die Gerade Y = X im ersten Quadranten würde dann die Genauigkeit der Messung repräsentieren, also die ideale Kombination aus hoher Richtigkeit und hoher Präzision.

Referenzwert oder wahrer Wert?

Zu Beginn dieses Artikels wurde der Referenzwert als wahrer Wert betrachtet. Der Grund dafür liegt in den Spezifikationen der Referenzstromquelle, die für unsere Zwecke als exakt angenommen wurde.

In Wirklichkeit jedoch, und das könnte Sie enttäuschen, existiert der wahre Wert einer physikalischen Größe zwar theoretisch, ist jedoch in der Praxis unbekannt und nicht exakt bestimmbar, da jede Messung zwangsläufig mit einer Unsicherheit größer als null behaftet ist,

oder anders ausgedrückt:

• Der wahre Wert ist ideal, aber rein theoretisch – die exakte Bestimmung ist unmöglich.
• Der Referenzwert ist der bestverfügbare Näherungswert und dient in praktischen Messsituationen als (lokaler) Standard.

Die zentrale Aufgabe der Metrologie besteht genau darin, die Differenz zwischen wahrem Wert und gemessenem Wert so weit wie möglich zu minimieren.

Diese Annäherung erfolgt durch den Einsatz von Kalibrierstandards mit zunehmender Genauigkeit, die gemeinsam die sogenannte Rückführbarkeitskette eines Messinstruments bilden . Dieser Themenbereich, ebenso wie viele weitere Aspekte zu Erfassungs- und Ablesefehlern bei elektronischen Messgeräten, wird in einem zukünftigen Artikel vertieft behandelt.

Anmerkung der Redaktion: Dieser Artikel (250046-02) erschien in der Ausgabe Mai/Juni 2025 von ElektorMag.

Sie haben Fragen oder Anmerkungen?

Haben Sie technische Fragen oder Kommentare zu diesem Artikel? Dann schreiben Sie bitte direkt an den Autor unter roberto.armani@elektor.com oder wenden Sie sich an die Elektor-Redaktion unter redaktion@elektor.de.